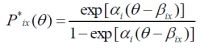Métodos de Inferencia

SAMUEL determina el conocimiento del alumno acumulando las distintas evidencias (por ejemplo, calificaciones obtenidas en las distintas actividades) que va recibiendo. Esta acumulación puede ser configurada de varias maneras explicadas a continuación.

Las operaciones del servicio web de SAMUEL destinadas a obtener el conocimiento del alumno (requestKnowledge y requestKnowledgeWeighted) tienen, entre otros, los siguientes parámetros:

• date: fecha para la que se desea consultar el conocimiento del alumno
• windowSize: tamaño de ventanas (en días o en número de evidencias, según el parámetro windowType) en la que se asume que el conocimiento no cambia
• windowType: tipo de ventana: 1 para ventana tipo número evidencia y 2 para ventana tipo número de días
• method: método de acumulación de evidencias: 1 para Graded Responde Model y 2 para Bayes.

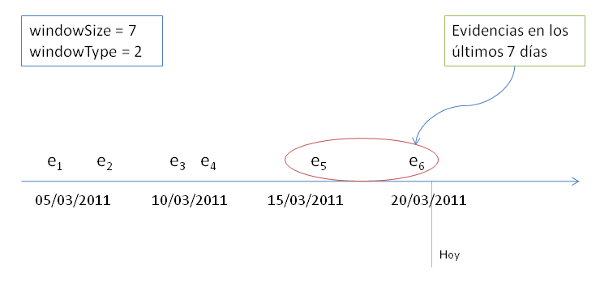
Por ejemplo, si queremos obtener el conocimiento de hoy usando las evidencias de los últimos 7 días, tendríamos date=fecha de hoy, windowSize=7 y windowType=2:

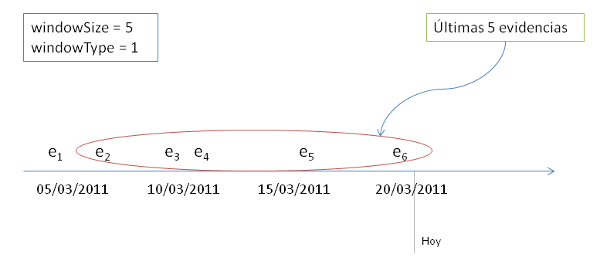
En cambio, si queremos obtener el conocimiento de hoy usando las últimas 5 evidencias, tendríamos date=fecha de hoy, windowSize=5 y windowType=1:

Por último, el parámetro method indica el método de acumulación que SAMUEL utilizará para acumular las evidencias (filtradas según los mecanismos anteriores) y así obtener el conocimiento del alumno. En la versión 1.1 de SAMUEL, el método de acumulación disponible es Graded Responde Model(method=1), el cual explicamos más detalladamente en el siguiente punto.

Graded Response Model

Graded Response Model (GRM) es un modelo IRT para respuestas al item con más de 2 categorías (ordenadas) de respuesta en función del grado de resolución del problema. Para cada item i hay un número de categorías de respuesta igual k_i.

• Sea θ el rasgo latente.
• X_i, variable aleatoria que indica la respuesta al item graduado i.
• x = 0,..,k_i-1 las respuestas actuales.

Lo que queremos obtener es:

P_ix(θ) = P_i(X = x | θ)

Es decir, la probabilidad de obtener la respuesta x (calificación) en el item i (actividad) teniendo un conocimiento θ. Esta probabilidad se obtiene en dos pasos:

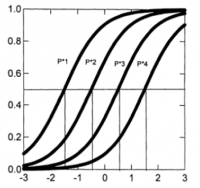
• Cálculo de las "Operating Characteristic Curves" (OCC) o curvas características.

Son k_i curvas de la forma:

• donde P^*_ix = P_i(X ≥ x | θ), para x=1,..,k_i-1 es decir, la probabilidad de, teniendo un conocimiento θ, obtener una calificación mayor o igual que x
• α: discriminación del item
• β: k_i -1 parámetros de dificultad
• por definición, P^*_i0=1 y P^*_iki=0.
  • Ejemplo: para α_j = 1.5, β_j1 = -1.5, β_j2 = -0.5, β_j3 = 0.5, β_j4 = 1.5
    

• Cálculo de las "Category Response Curves" (CRC) o curvas de respuesta.

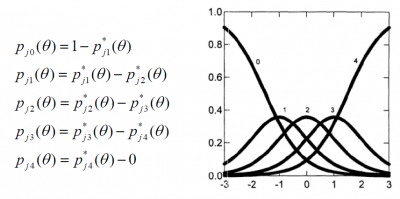
Una vez estimadas las k_i-1 curvas OCC, la probabilidad de responder en las categorías x=0,1,...,k_i-1 se calcula como: P_ix(θ) = P^*_ix(θ)-P^*_ix+1(θ)

• Ejemplo:
  

GRM en SAMUEL

La principal dificultad del modelo GRM es la de determinar los parámetros α y β. Existen algoritmos que usan métodos de máxima verosimilitud para ajustar dichos parámetros, pero para ello sería necesario disponer, por cada actividad, de una cantidad adecuada de calificaciones previas.

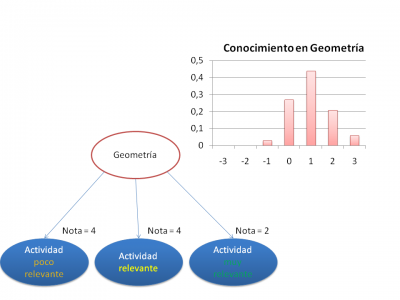
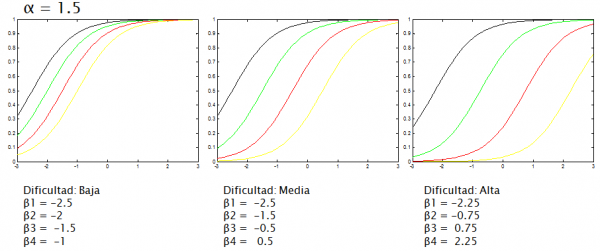
En la versión actual de SAMUEL, el parámetro α es un parámetro de configuración y el parámetro β se determina mediante un heurístico en función de la dificultad o relevancia establecida por el profesor para cada actividad. Por ejemplo, para actividades con cinco calificaciones posibles (0...4) SAMUEL generaría las siguientes curvas características para un α = 1.5 y un θ entre -3 y 3:

.

Obteniendo las siguientes curvas de respuesta:

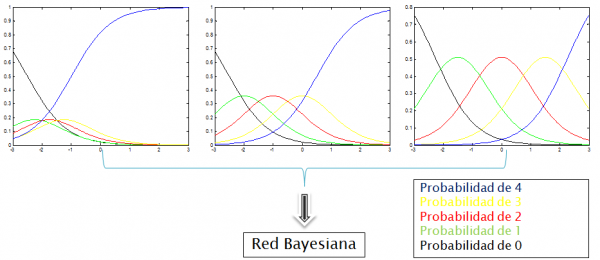
Finalmente, lo que tenemos es una red bayesiana configurada con las probabilidades que obtenemos de las curvas de respuesta, de manera que SAMUEL infiere el conocimiento del alumno calculando las probabilidades a posteriori dadas las distintas evidencias de las distintas actividades, y asumiendo un conocimiento inicial del alumno equiprobable: